Antek L. - 1990

DZIEŁO JANUSZA MORDASEWICZA

Zwróciło się do mnie kilka osób abym opowiedział, co tak właściwie odkrył Janusz Mordasewicz. Postanowiłem opowiedzieć jak to wszystko widzę, choć wiem, że moja interpretacja będzie zawierać elementy krytyczne. Wytłumaczenie, dlaczego nie odniósł sukcesu może być potraktowane jako wskazanie czego nie odkrył i nie zrozumiał. Sądzę jednak, że jestem jedyną osobą mogącą w pełni zrozumieć i docenić jego zmagania i osiągnięcia, dlatego zgodziłem się zabrać głos.

Inżynier Janusz Mordasewicz skonstruował cieplnicę i odkrył, że umożliwia ona w określonych warunkach w 100% zamianę ciepła na pracę, czyli budowę perpetuum mobile II rodzaju. Została opatentowana pod nr 104402 (zgłoszenie 188482) jako "Pompa ciepła napędzana ciepłem i pracą".

Jednak cieplnica nie może być uważana za pompę ciepła jeśli entropię będziemy pojmowali jak dotychczas, a dramat pana Janusza polegał na tym, że zdał sobie z tego sprawę zbyt późno. Ale po kolei.

O początkach cieplnicy pisał tak:

Dawno, dawno temu, kiedy byłem studentem obserwowałem krople wody zbierające się na spodzie talerzyka przykrywającego małą czarną w szklance. Myślałem wówczas jak to by było dobrze, gdyby udało się zmusić parę do przeniesienia utajonego ciepła parowania i oddanie go w wyższej temperaturze. Musiałem wiele lat czekać na okazję przeprowadzenia odpowiednich doświadczeń, ale udało się, skonstruowałem działającą pompę ciepła. Jej wydajność był niewielka, natomiast sprawność... większa od sprawności Carnota. W tej sytuacji odważyłem się na obrazoburczą publikację "Czy założenia prowadzące do sformułowania II zasady termodynamiki są jednoznaczne i niezachwiane?" w Energetyce Przemysłowej nr 12/62. Piszę 'obrazoburczą', bo jedynym jej efektem było określenie mnie heretykiem.

Teraz gdy znamy genezę cieplnicy, zapoznajmy się bliżej z jej konstrukcją.

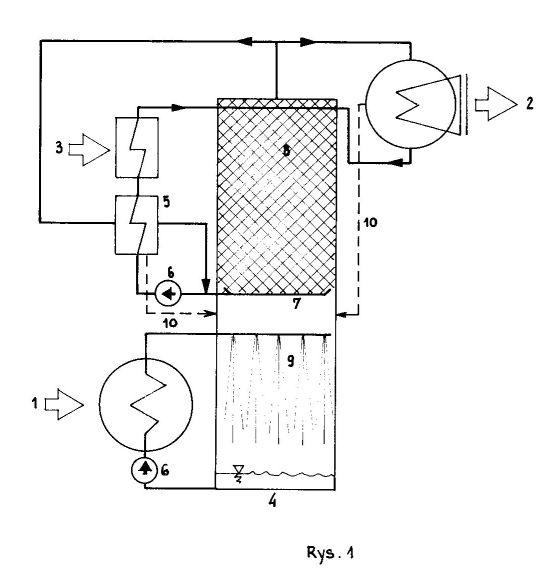
1. Ciepło doprowadzane

2.Ciepło odprowadzane

3.Ciepło napędowe

4. Kolumna cieplnicy

5. Podgrzewacz regeneracyjny

6. Pompy obiegowe

7. Rynny przelewowe

8. Siatki ociekowe

9. Dolny zraszalnik

10. Powietrze resztkowe

Cieplnica składa się z pionowej kolumny, w której zachodzi główny proces i urządzeń towarzyszących mających za zadanie zapewnić obieg czynnika. rys.(1) W górnej części kolumny wprowadzana jest gorąca woda, która ścieka po siatkach. Z dołu do góry przenika para wodna przez gaz wypełniający kolumnę. Woda ściekając stygnie i odparowuje, a para przenikając do góry nagrzewa się i zagęszcza. Z opisu wynika, że kolumna jest przeciwprądowym wymiennikiem ciepła i masy. W całej kolumnie jest stałe ciśnienie cząstkowe pary, choć na każdym poziomie jest inne - odpowiada ciśnieniu cząstkowemu pary nasyconej dla danej temperatury. Głównym zadaniem cieplnicy jest podgrzać utrzymując w stanie nasycenia, parę wydzieloną u dołu kolumny.

Krytykę z jaką spotkała się cieplnica można podzielić na dwa etapy. W pierwszym wskazywano, że procesy opisywane w artykule nie mogą w niej zajść. Doprowadziło to do pomiaru wykonanego na modelu cieplnicy przez Energopomiar w 1964 roku. Pomiar ten był bardzo ważny, bo pokazał, że para przenikała jednak do góry transportując ciepło (choć suma entropii całego modelu była większa od zera).

Jest jeszcze jeden irytujący moment tej historii: już Arystoteles zauważył, że gorąca woda szybciej marznie niż zimna. W latach sześćdziesiątych XX wieku w afrykańskiej wsi, pomocnik cukiernika Mpemba, kilka razy spiesząc się na jakieś spotkanie, nie zostawił garnka z gorącą mieszaniną do produkcji lodów na wierzchu, tylko wstawił ją do lodówki. Zauważył, że ta mieszanina szybciej zamieniła się w lody niż mieszanina wstawiona do lodówki jako zimna. Wraz ze swoim profesorem napisali artykuł do Science, który uczynił ich sławnymi. Zjawisko to naukowcy "wyjaśnili" dopiero w 2013 roku. Piszę "wyjaśnili", bo gdyby naprawdę zrozumieli, to wiedzieliby jak to zjawisko wykorzystać!

W drugim etapie nie krytykowano opisu procesów. Wszystkie teorie pana Janusza: "względnych i bezwzględnych źródeł ciepła", "obiegów dwustrumieniowych" i "V zasada termodynamiki" będące kolejnymi próbami określenia warunków w jakich może dojść do malenia entropii, spotykały się z krytyką za samo twierdzenie o możliwości jej malenia.

Przez długie lata pan Janusz uważał, że główną siłą sprawczą umożliwiającą zachodzenie procesów w cieplnicy jest ziemskie pole grawitacyjne. Nie potrafił tego jednak wykazać rachunkowo. Dopiero zetknięcie bliżej z pracami prof. I. Prigogine'a sprawiło, że na entropię spojrzał inaczej.

I tu zaczyna się właściwa opowieść o tym co odkrył Janusz Mordasewicz, bo moim zdaniem ważniejsza od wiedzy jak działa cieplnica jest wiedza dlaczego ona działa. Ta bowiem wiedza pozwala INACZEJ rozumieć entropię i umożliwia określenie kiedy może w układzie maleć.

Żeby jasne było co rozumiał przez entropię przytoczę jeszcze jeden duży fragment opracowania pana Janusza przedstawiający historię rozwoju pojęcia entropii.

...Jej historia zaczęła się na początku XIX wieku, kiedy Leonard Sadi Carnot próbował określić relację jaka zachodzi między ilością ciepła dostarczonego maszynie, a ilością uzyskanej z niego pracy. Pojęcie ciepła nie było jeszcze wówczas tak sprecyzowane jak dzisiaj i Carnot w swej pracy posłużył się terminem "caloryk", pochodzącym od Lavoisiera. Potraktował różnicę temperatur między kotłem a skraplaczem maszyny parowej jak różnicę poziomów wody u szczytu i podnóża wodospadu. Stąd ilość możliwej do uzyskania pracy widział jako iloczyn tej różnicy temperatur i ilości dostarczonego kaloryka. W tak rozumianych obliczeniach kaloryk nie przedstawiał energii, lecz wielkość, którą w przyszłości Clausius nazwał entropią. Carnotowi oprócz sformułowania problemu sprawności termicznej udało się wykazać, że największą sprawność będzie miała maszyna działająca bez strat a więc jak to określił - odwracalnie.

W połowie XIX wieku problematyką ciepła zajął się Rudolf Clausius, który sprecyzował pojęcie ciepła i sformułował pierwszą zasadę termodynamiki. Potem zebrawszy prace Carnota, Clapeyrona oraz Kelvina, wyprowadził z nich drugą zasadę termodynamiki, której nadał postać całki kołowej z funkcji nazwanej przez siebie entropią. Stało się wówczas jasne, że urządzenie zamieniające ciepło na pracę może mieć tylko ograniczoną sprawność, zależną jedynie od temperatury grzejnika i skraplacza. Z własności entropii wynikało, że jej wartość nie zależy od rodzaju czynnika i, że w układach odosobnionych musi w czasie przemiany wzrastać. Było to konsekwencją przepływu ciepła (ex definitione) ze spadkiem temperatury i tarcia (nieuniknionego). Clausius ogłosił też wnioski filozoficzne wynikające z drugiej zasady: wszystkie przemiany w przyrodzie, w których bierze udział ciepło są nieodwracalne. Temperatury się wyrównują a Wszechświat czeka w dalekiej przyszłości śmierć cieplna.

Ogłoszenie drugiej zasady termodynamiki spowodowało ujawnienie sprzeczności przy zestawieniu jej z mechaniką klasyczną. Równania mechaniki były odwracalne ze względu na czas - po zmianie czasu na ujemny równania opisywały przebieg wydarzeń wstecz, czyli żaden kierunek przebiegu zdarzeń nie był wyróżniony. Zrozumienie, że druga zasada wyróżnia kierunek przepływu czasu a mechanika nie, zapoczątkowało długie spory w świecie fizyków i filozofów, które dopiero prace Ludwiga Boltzmanna pomogły rozstrzygnąć. W 1872 roku ogłosił swoje słynne twierdzenie H, które orzekało, że entropia nie maleje. W twierdzeniu tym H można utożsamić z entropią termiczną, mimo, że zostało ono wyprowadzone w oparciu o model mechaniczny. Pogodzenie sprzeczności możliwe było na gruncie interpretacji statystycznej: wszystkie rozkłady elementarne są równie prawdopodobne, ale rozkłady o większej entropii mogą być realizowane na więcej sposobów i dlatego są w sumie bardziej częste. Od tej chwili pozycja drugiej zasady była ugruntowana, choć nie rozumiano jej tak kategorycznie jak poprzednio. Do czasu.

W pierwszych latach XX wieku prace Waltera Nernsta wykazały, że entropia wyliczona w oparciu o model gazowy, jak w równaniu H Boltzmanna, jest nie do pogodzenia z zachowaniem faz skondensowanych w pobliżu zera bezwzględnego. Zaowocowało to wprowadzeniem do termodynamiki trzeciej zasady głoszącej, że w zerze bezwzględnym należy przyjmować entropię równą zero. W rezultacie dzisiaj godzi się te zasady stwierdzeniem, że druga zasada pozwala wyliczyć przyrosty entropii i określić kierunek przemiany a trzecia pozwala wyznaczyć jej wartość bezwzględną.

W tym samym czasie C. Caratheodory pokusił sie o bardziej klarowne (z punktu widzenia teorii) przedstawienie termodynamiki. Stwierdził, że nie jest potrzebne pojęcie ciepła jako osobnej formy energii. Wystarczy stwierdzenie, że jest to różny od pracy przekaz energii wewnętrznej. Ale ani przekaz energii drogą pracy, ani ten drugi sposób nie jest różniczką zupełną, czyli zawsze zależą one od drogi przemiany. Caratheodory stwierdził, że istnieją przemiany graniczne, jednak nie to jest ważne dla naszych rozważań, a tylko fakt, że przemiany te są zawsze kolejnymi stanami równowagi.

Uświadomienie sobie przez fizyków, że opis termodynamiki klasycznej nie nadaje się do analizy układów nie będących w stanie równowagi termodynamicznej wymusił sformułowanie nowego formalizmu nazwanego termodynamiką nierównowagową. Formalizm ten radykalnie różni się od stosowanego w termodynamice klasycznej: przestrzeń stanów jest zastąpiona przestrzenią fizyczną, a czynnik fenomenologiczny, materią o budowie cząstkowej. Pojawiają się "źródła entropii", które nie mają analogii w termodynamice klasycznej. Gradient wielkości intensywnych wywołuje przepływy, czyli procesy nieodwracalne. Iloczyn takiego "bodźca" termodynamicznego i skoniugowanego z nim przepływu jest traktowany jako źródło entropii.

Przepływy mogą się sumować lub niwelować poprzez procesy sprzężone. Gdy np. dochodzi do przepływu ciepła, to może zdarzyć się, że w układzie wywoła on przeciwnie skierowany przepływ składników powodujący powstanie gradientu stężeń. Termodynamika nierównowagowa najefektywniejszych modeli dostarcza dla stanów układu ustalonych w czasie i niewiele odchylonych od stanu równowagi. Spełniony jest wówczas w pełni postulat lokalnej równowagi komórkowej konieczny dla stosowania liniowych metod obliczeniowych.

Trzeba zdawać sobie sprawę, że identyczność entropii klasycznej i nierównowagowej jest względna, podobne jak względne jest pojęcie ruchu. Entropia klasyczna przepływa razem z ciepłem lub czynnikiem, natomiast entropia nierównowagowa jest produkowana lokalnie. W teorii klasycznej są układy, których entropia może maleć kosztem innych, w których rośnie - w nierównowagowej rośnie wszędzie, ale za to istnieją procesy w których entropia może maleć kosztem wzrostu w innych procesach (zachodzących w tym samym obszarze). W termodynamice klasycznej ostateczny bilans dotyczy tylko źródeł ciepła; w nierównowagowej określany jest wzrost entropii układu. Termodynamicy klasyczni przystępując do badań wyodrębniają z otaczającego go świata układ który badają, a resztę nazywają otoczeniem. W teorii klasycznej nie precyzuje się takich parametrów otoczenia (czyli źródła ciepła) jak skład chemiczny, objętość czy ciśnienie a jedynie określa się temperaturę. Mocno podkreśla się przy tym, że wszystkie ustalenia teorii klasycznej dotyczą tylko układów zamkniętych. Termodynamicy nierównowagowi wyodrębniając układ badany, większą uwagę zwracają na granice tego układu. Układ taki może się przemieszczać a przez jego ścianki mogą przepływać substraty, produkty i substancje obojętne, ale to co dzieje się poza układem, termodynamików nie interesuje. Jednak mimo tak elastycznego podejścia do badań, termodynamika układów żywych wydawała się sprzeczna.

W roku 1937 na Uniwersytecie w Chicago, wiedeński biolog Ludwig von Bertalanffy po raz pierwszy przedstawił zarys ogólnej teorii systemów. Pokazał, że niektóre systemy otwarte, takie jakimi są np. zwierzęta, działają wbrew drugiej zasadzie termodynamiki w sensie wzrostu entropii chemicznej. Chociaż wszystkie przemiany ustroju przebiegają ze spadkiem charakteryzujących je parametrów, to jednak ogólnie biorąc entropia organizmu nie rośnie. Paradoks ten nie rozwiązany był aż do prac Ilyi Prigogine'a, który wykazał, że pewne układy otwarte (nazywane strukturami dysypatywnymi) są w termodynamice czymś wyjątkowym i chcąc uniknąć sprzeczności trzeba je traktować inaczej, niż czyniła to termodynamika ze zwykłymi układami przepływowymi. Struktury dysypatywne, czyli układy otwarte trzeciej klasy, charakteryzują się wymianą materii i energii z otoczeniem, jak również zachodzeniem w ich obrębie przemian dalekich od stanu równowagi. Przemiany te są we wzajemnej równowadze dynamicznej i cechują się wzajemnym uwarunkowaniem, tak, że Prigogine nazwał je procesami sprzężonymi. Np. w żywym organizmie procesy sprzężone prowadzą z jednej strony do dezorganizacji wysokoenergetycznych składników pożywienia a z drugiej dzięki nim przebiegają procesy umożliwiające funkcje ruchowe i budulcowe organizmu. Struktury dysypatywne są układami w których nie da się stosować metod liniowych, gdyż procesy sprzężone są dla siebie nawzajem "układami odniesienia". Nieprzydatna jest w nich zasada przemienności Onsagera, gdyż struktury te są anizotropowe, mimo stacjonarności zachodzących w nich procesów. Termodynamice struktur dysypatywnych udało się ustalić, że mimo, iż w stanie stacjonarnym produkcja entropii jest minimalna, istnienie struktury uzależnione jest od dopływu energii (ujemnej entropii) z zewnątrz.

...Podsumujmy. Termodynamika klasyczna analizuje przyrosty entropii źródeł, termodynamika nierównowagowa oblicza produkcję entropii w układzie, teoria struktur dysypatywnych usiłuje uzgodnić bilans wzrostu entropii w procesach sprzężonych z przyrostem entropii otoczenia.

W tym miejscu kończy się wiedza jaką otrzymujemy na uczelni a rozpoczyna świat otwarty przez Janusza Mordasewicza. W ostatnim zdaniu cytatu użyty został zwrot "usiłuje uzgodnić" i sądzę, że użyty trafnie. Termodynamika struktur dysypatywnych mogłaby być teorią względności w termodynamice gdyby odkryła, że tych dwóch entropii uzgodnić się nie da.

Między nimi zachodzi określona relacja ale nie zachodzi zgodność. Aby to bliżej wyjaśnić trzeba przyjrzeć się narzędziom pojęciowym, którymi posługują się dzisiaj fizycy.

Najwygodniej będzie zacząć od początku czyli od Arystotelesa. Jego nauka o przyrodzie czyli "fizyka" nie obejmowała zespołu zagadnień podstawowych będących poza jej zasięgiem, określonych mianem "metafizyki". Podział ten odzwierciedlał problem rozróżnienia tego co poznajemy zmysłami, od tego co poznajemy rozumem. Z tym problemem wiązał się problem rozróżnienia poznającego, czyli podmiotu i przedmiotu poznania. Krótko mówiąc już w starożytności zaczął się problem SYTEMU i jego OTOCZENIA. Pojawił się w związku z poszukiwaniem MĄDROŚCI, to jest ostatecznej - bez odwołania się do nauk wyższych - teorii rzeczywistości. Mądrości, czyli wiedzy absolutnej, systemu bez otoczenia.

W średniowieczu trzy wspomniane elementy zostały przez św. Tomasza określone jako nauki realne (oparte na empirii), nauki formalne (oparte na pojęciach logiczno-matematycznych) i filozofię (bazującą na metafizyce). Czasy Bacona i Kartezjusza wzięły rozbrat z metafizyką. Od tej chwili mądrość nie była potrzebna. WIEDZA posługująca się metodą determinowała ludzkie poznanie. Wiedza tworzyła teorię rzeczywistości opierając się na eksperymencie, a o tym co wskazywał eksperyment mówiła teoria. Wiedza teoretyczna zaczęła doznawać wsparcia od eksperymentu i sprawiała, że zjawiska dawniej nieprzewidywalne znalazły się w zasięgu predykcji. Choć w tamtych czasach wybitni matematycy byli równocześnie wybitnymi fizykami, bardzo powoli rodziła się świadomość, że wieloznaczny język codzienny i precyzyjna naukowa terminologia to nie to samo. Ponieważ nie tylko zwykli ludzie ale i uczeni zaczęli tracić orientację gdzie kończy się model a zaczyna "rzeczywistość", rozgorzała walka o określenie co jest naukową teorią a co zwykłą spekulacją. Zaczęto zdawać sobie sprawę z trzech faktów:

- teoria jest tylko modelem rzeczywistości,

- każda z istniejących teorii opisuje tylko jej część,

- różne modele działają przy różnych założeniach, a sensowność teorii i tym samym założeń, musi być potwierdzona eksperymentalnie.

Pierwszą wielką teorią fizyczną, która znalazła pełne odzwierciedlenie w matematyce była teoria grawitacji. Newtonowi udało się przenieść na grunt matematyki takie pojęcia jak przestrzeń, energia i siła. Było to wówczas bardzo zadowalające z filozoficznego punktu widzenia, bo tak jak przestrzeń wydawała się nieskończona tak aż do nieskończoności działał rachunek.

Druga fundamentalna teoria w której oddziaływanie, jak w grawitacji, zmienia się z kwadratem odległości, to elektrostatyka. Obydwie łączy wspaniała matematyczna teoria równań różniczkowych cząstkowych rzędu drugiego, nie potrafiąca jednak powiedzieć czym w istocie różnią się te siły. Siły są takie same, lecz nie te same. Oznacza to, że jakościowo są nierozróżnialne a ilościowo różnią się stałą pomiarową wprowadzoną do teorii z zewnątrz. Można porównywać ilość energii zmieniającą się pod ich wpływem ale nie można dodawać samych sił. Ponieważ matematycznie siły te można dodać, choć fizycznie jest to bez sensu, zajmujemy się teraz nie metafizyką tylko matematyką tych teorii - tym bardziej, że jest dla nich wspólna.

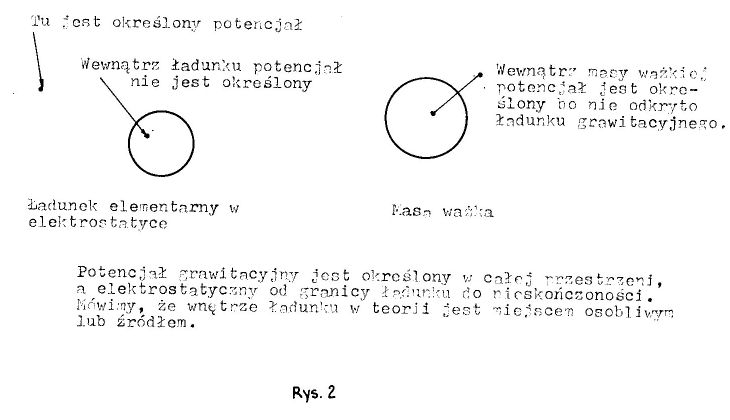
Siły grawitacyjne są 10⁴⁰ razy słabsze od elektrostatycznych, nie powinno nas zatem dziwić, że choć udało się oznaczyć wielkość elementarnego ładunku elektrycznego nie powiodło się to w grawitacji. Ale tego ładunku elektrycznego nie potrafimy nijak określić, bo właściwie teoria matematyczna nie przewiduje istnienia ładunku elementarnego. Potrafimy za to porównywać siły z jakimi na siebie oddziałują różne ładunki, i w ten sposób możemy określać ich wielkość. Mówimy wówczas, że potrafimy wyznaczyć pole sił wokół ładunku - od nieskończoności po nieskończoność. Analogiczne pole sił możemy wyznaczyć wokół masy ważkiej. Praca jaką trzeba włożyć by ładunki do siebie zbliżyć "z nieskończoności" określana jest jako energia potencjalna. Gdybyśmy każdemu punktowi przestrzeni z rozmieszczonymi ładunkami przypisali liczbę równą takiej pracy przemieszczenia, powiedzielibyśmy, że została określona funkcja przestrzenna zwana potencjałem.

Ma ona ciekawą własność. Okazuje się, że nie ważne jaką drogą przemieszczamy poszczególne ładunki - wartość tej pracy zależy tylko od punktu początkowego i końcowego takiego przesunięcia. Potencjał przestrzenny ma kilka takich ważnych własności, zatem warto mu się przyjrzeć bliżej. Funkcja ta jest określona w pustej przestrzeni POZA ładunkami, i w miarę oddalania od ładunków jej wartość maleje. (rys.2).

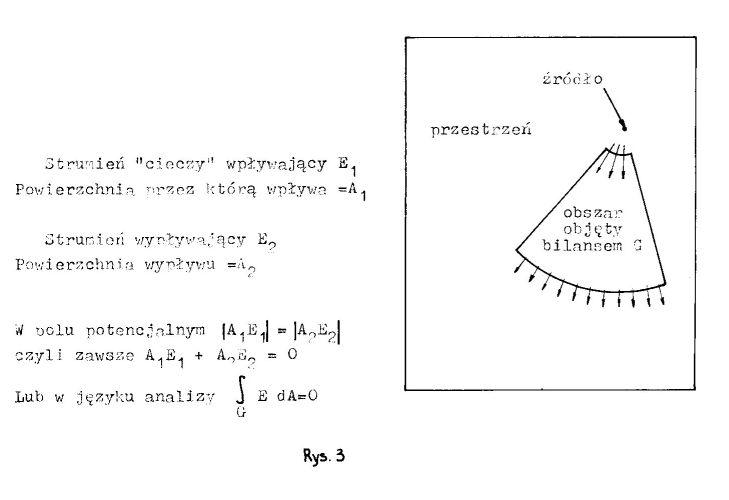
Zauważono, że liczbowo, szybkość spadku tej wartości jest jak gdyby równa wypływowi nieściśliwej cieczy z ładunków jak ze źródeł. A więc obojętnie jak otoczymy badany ładunek (lub ładunki) osłoną bilansową, wypływ tej "cieczy" będzie taki sam. Bliżej ładunku otaczająca powierzchnia będzie mała a prędkość przepływu duża, a dalej od ładunku powierzchnia bilansowa będzie większa a prędkość mniejsza tak, że przepływający strumień będzie stały. Zwróćmy jednak uwagę, że ponieważ potencjał nie obejmuje źródeł, bilans jego osłony jest zerowy - to co wpływa do osłony to z niej wypływa.(rys.3)

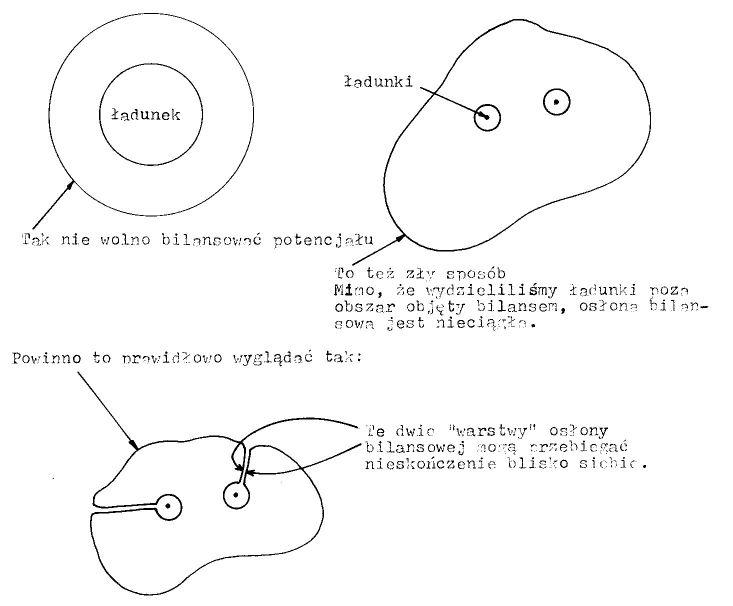
Takie zdefiniowanie potencjału określa go od źródeł do nieskończoności, mimo to w zastosowaniach interesuje nas obszar ograniczony. (rys.4)

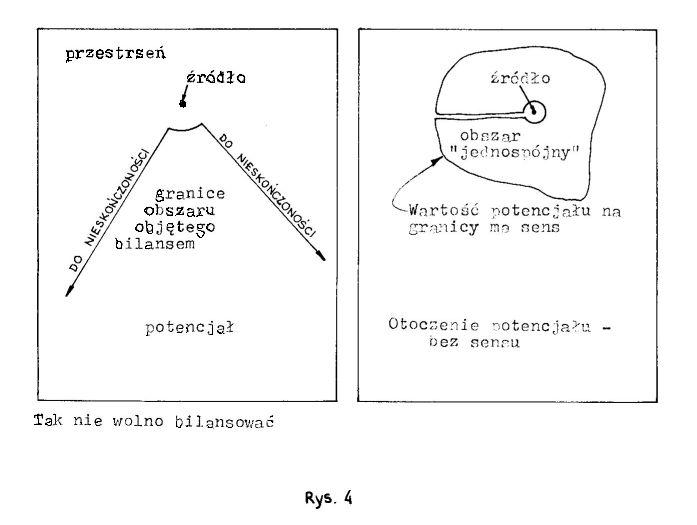
A to oznacza, że pojęcie "otoczenie potencjału" jest i dla matematyka i dla fizyka bez sensu. Wartość potencjału na granicy całkowicie określa to co dzieje się w obszarze. Właśnie ta cecha nadaje potencjałowi tak duże znaczenie. Tak jak nie można wyobrazić sobie otocznia potencjału tak nie można sobie wyobrazić pozaprzestrzeni, a więc twierdzenia odnoszące się do potencjału mają cechę absolutności. Chcę przez to powiedzieć, że nie dysponujemy ŻADNĄ metodą rachunkową łączącą własności potencjału z "pozapotencjałem". Mówiąc inaczej, nasze wnioski o bezkresnym działaniu sił fizycznych opieramy całkowicie na teorii matematycznej a nie pomiarach.

Tu powinienem wspomnieć, że do określenia tego co dzieje się w obszarze w relacji z otoczeniem służy twierdzenie Ostrogradskiego-Gaussa o divergencji (rozbieżności). Twierdzenie o divergencji mówi, że gdybyśmy podzielili cały obszar na malutkie objętości to wszystkie zachowywałyby się jakby w nich były "źródła" lub "upusty". A więc w dowolnie wybranym obszarze potencjału suma źródeł i upustów musi dawać zero.

Zwróćmy uwagę, że "źródło" zostało ujęte w cudzysłów, bo divergencja jest tylko matematyczną sztuczką, która pozwala nam badać wypływ "cieczy" objętościowo w przeciwieństwie do metody badania strumienia przepływającego przez powierzchnię.

Te dwie metody mają się do siebie jak termodynamika klasyczna i termodynamika nierównowagowa. Termodynamika skorzystała z tego wspaniałego narzędzia jakim jest teoria potencjału w momencie, gdy zauważono, że entropia spełnia wszystkie cechy potencjału. Czynnik roboczy w siłowni cieplnej przechodzi różne przemiany termodynamiczne (mówimy - zmiany stanu) od kotła poprzez turbinę, skraplacz, podgrzewacz, by znaleźć się znów w kotle. Właśnie ta cykliczna zmiana stanu czynnika roboczego sprawia, że można ją przedstawić jako cykl kołowy.

Spostrzeżenie zaś, że ciepło zredukowane, czyli podzielone przez temperaturę bezwzględną, pełni rolę analogiczną do cieczy w teorii potencjału, pozwoliło przenieść wszystkie wnioski z teorii już poznanej i przebadanej. Pierwszy i najważniejszy to bezgraniczność zasięgu. Jest jednak pewna zasadnicza różnica pomiędzy potencjałem elektrostatycznym i grawitacyjnym a entropią. Tamte dwa są potencjałami zdefiniowanymi w przestrzeni FIZYCZNEJ a entropia jest określona w przestrzeni STANÓW. Dla fizyka siła jest zjawiskiem REALNYM a potencjał jedynie matematyczną podpórką.

Natomiast ciśnienie będące parametrem stanu jest abstraktem na który mają wpływ obydwie, różne fizycznie siły. Można np. zademonstrować, iż ciśnienie w cieczy przyjmuje wartość ujemną tj. poniżej próżni! Dlatego fizycy bardzo mocno podkreślają, że koronne sformułowanie termodynamiki klasycznej podane jest (przez Caratheodorego) dla dokładnie przebadanych eksperymentalnie, układów izolowanych.

Potencjalne pole sił ma pewną cechę z której nie zawsze zdajemy sobie sprawę: fizyczny, przestrzenny rozkład źródeł ukształtowany jest siłami pozapotencjalnymi (z wyjątkiem pojedynczego ładunku elementarnego, którego strukturę zbudowała sama Natura). Ta cecha sprawia, że prawdziwe niespodzianki można znaleźć przy badaniu rozkładów źródeł na krzywych powierzchniach w przestrzeniach anizotropowych (tj. takich, które maja różne własności w różnych kierunkach), lub przy ruchu źródeł. Taką wielką niespodziankę odkrył prof. I. Prigogine badając pod kątem własności termodynamicznych przepływ substancji i energii przez organizmy żywe. Spostrzegł mianowicie, że we wspomnianych strukturach dysypatywnych, które charakteryzują się "więzami wewnętrznymi" obieg substancji i energii jest wielostronnie wzajemnie uwarunkowany. A to oznacza, że przemiany nazwane przez niego sprzężonymi są NIELINIOWE. Dla matematyka wnioski są natychmiastowe: przemiany NIE są potencjalne, bo potencjał z definicji jest funkcją liniową, ale co to oznacza dla fizyka?

Dla Janusza Mordasewicza było to objawienie. Wreszcie po wielu latach poszukiwań znalazł dziurę w potencjale, tzn. odkrył w jaki sposób entropia może maleć. W obiegu cieplnicy czynnik ulega przemianom kołowym, ale nie można ich zobrazować na wykresie p,T,V. Trzeba by się zgodzić albo, że przestrzeń jest anizotropowa albo, że przemiana jest otwarta. I tu w sukurs przyszło odkrycie profesora I. Prigogine'a.

Jeżeli przyjmiemy, że przemiany jakim ulegają spływająca w dół woda i unosząca się para są przemianami sprzężonymi, to przedstawiają je dwie krzywe leżące na "powierzchni nasycenia" lecz nie w przestrzeni p,T,V tylko w przestrzeni p,V,m (rys.5)

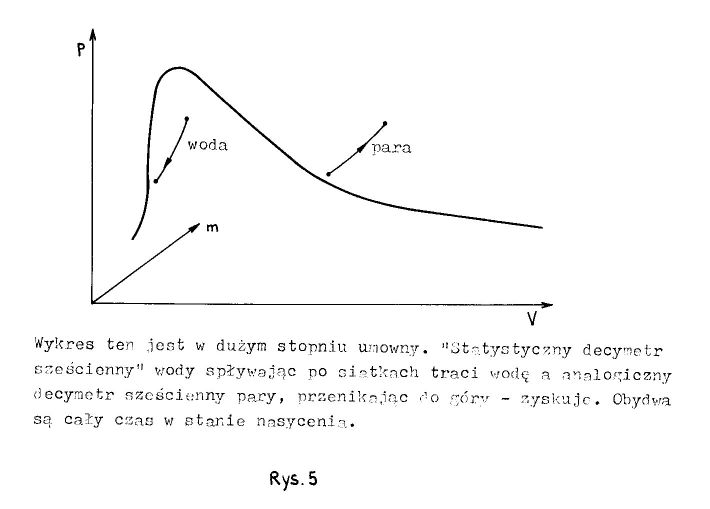
jednak wówczas entropia otoczenia cieplnicy może maleć: oczywiście z punktu widzenia II zasady termodynamiki taka przemiana nie może mieć miejsca.

I to był dramat pana Janusza. Taka przemiana ZACHODZIŁA w trzech różnych badanych modelach cieplnic, choć bilans entropii był dodatni. Niewłaściwie interpretując przez wiele lat przyczyny malenia entropii, pan Janusz źle prowadził doświadczenia, ale zdał sobie z tego sprawę zbyt późno. Grawitacja, która przez wiele lat była jego zdaniem siłą napędową cieplnicy - warunkuje i ma wpływ na szybkość procesu, ale nie na sprawność w sensie Carnota. Proces cieplnicowy jest silnie uzależniony od rodzaju czynnika i wielkości pola grawitacyjnego, bo jego istotą jest OTWARTOŚĆ PRZEMIANY. Jest nieporównywalny z obiegiem Carnota, choć ściany obiegu cieplnicy stanowią OBIEG ZAMKNIĘTY. Ja osobiście nie jestem przekonany, czy sposób obliczenia elementów cieplnicy stosowany przez pana Janusza jest właściwy, natomiast wiem, że odkrył NOWE ZJAWISKO.

Jego podstawowym polem wykorzystania jest energetyka zawodowa. Cieplnica umożliwia zawrócenie do obiegu i wykorzystanie ciepła, które jest wypuszczane do atmosfery przez chłodnie kominowe. W dalszej przyszłości będzie można robić to, co tak szokuje ludzi wychowanych na II zasadzie termodynamiki: studzić atmosferę i z niej czerpać energię. A potem...

Powyższy opis jest poprawny, ale nie daje wyobraźni pola do popisu. Powiedzmy wyraźnie: obiegi dwustrumieniowe nie dają się opisać teorią entropii. Opis obiegu dwustrumieniowego musi być czterowymiarowy, a w czterech wymiarach NIE DZIAŁA teoria potencjału (a zatem entropia traci sens). Obiegi dwustrumieniowe pozwalają "ominąć" prawa Newtona i sięgnąć po wolną energię, ale o tym szaaa!

Katowice 15.04.1990