mgr inż. Janusz Mordasewicz (1989)

CIEPLNICA

Cieplnica - pompa ciepła napędzana ciepłem i pracą
Patent 104402 z 1976 roku.


Dawno temu, kiedy byłem studentem, obserwowałem krople wody zbierające się na spodzie talerzyka przykrywającego małą czarną w szklance. Myślałem wówczas jak to by było dobrze, gdyby udało się zmusić parę do przeniesienia utajonego ciepła parowania i oddania go w wyższej temperaturze. Musiałem wiele lat czekać na okazję przeprowadzenia odpowiednich doświadczeń i pomiarów, ale udało się : skonstruowałem działającą pompę ciepła. Jej wydajność była niewielka, natomiast sprawność... większa od sprawności Carnota. W tej sytuacji odważyłem się na obrazoburczą publikację w "Energetyce Przemysłowej" nr 12/62 p.t. "Czy założenia prowadzące do sformułowania II-giej zasady termodynamiki są jednoznaczne i niezachwiane?" Piszę "obrazoburczą", bo jedynym jej efektem było określenie mnie heretykiem.

Mam wykształcenie inżynierskie a nie teoretyczne, dlatego drugą zasadę termodynamiki na początku lat sześćdziesiątych kojarzyłem raczej ze sprawnością zamiany ciepła na pracę niż z analizą entropową. Z tego powodu zakładałem, że klasyczna teoria Carnota jest "w zasadzie dobra", natomiast novum upatrywałem w odkryciu nowego typu obiegu, który nazwałem obiegiem dwustrumieniowym. W obliczeniach cieplnicy wykorzystywałem wartości entropii brane z tablic pary wodnej, natomiast strumienie pary i wody wyliczałem z bilansu energii. Jednak, gdy chciałem cieplnicą zainteresować innych, uparcie w dyskusji wracał argument oponentów: pomiary są błędne, gdyż teoria absolutnie nie dopuszcza globalnego malenia entropii. W tej sytuacji doszło do experimentum crucis jakim był pomiar wykonany w 1964 roku przez specjalistyczną firmę Energopomiar.

Pomiar ten pozwolił określić wszystkie charakterystyczne cechy procesu, ale nie dał pełnego obrazu możliwości cieplnicy. Poza tym nie przekonał oponentów, tym bardziej, że w owym czasie nie potrafiłem jeszcze powiedzieć, w jakich warunkach makroskopowych możemy mówić o maleniu entropii.

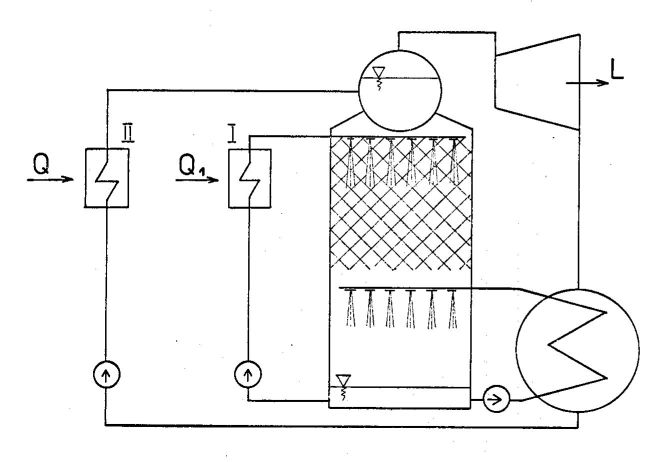
Tutaj pora na przedstawienie urządzenia.

Cieplnica składa się z pionowej kolumny w której zachodzi główny proces i urządzeń towarzyszących, mających za zadanie zapewnić obieg czynnika. W górnej części kolumny wprowadzana jest gorąca woda, która ścieka w dół po siatkach. Z dołu do góry przez gaz wypełniający kolumnę przenika para wodna wydzielona w obszarze dolnego zraszalnika. Woda ściekając stygnie i odparowuje a para przenikając do góry nagrzewa się i zagęszcza. Z opisu wynika, że kolumna jest przeciwprądowym wymiennikiem ciepła i masy. W całej kolumnie jest stałe ciśnienie, lecz ciśnienie cząstkowe pary na każdym poziomie jest inne - odpowiada ciśnieniu cząstkowemu pary nasyconej dla lokalnej temperatury wody. Głównym zadaniem cieplnicy jest podgrzać utrzymując w stanie nasycenia parę wydzieloną z dołu kolumny.

Kiedy przedstawiałem termodynamikom schemat cieplnicy do analizy, przeważnie stwierdzali, że to chyba niemożliwe aby opisany proces mógł zajść. Chłodna para nie może przenikając do góry podgrzać się i zwiększyć ciśnienie cząstkowe wbrew gradientowi temperatury i stężenia.

A jednak ten zdumiewający proces zachodzi i jest potwierdzony pomiarami! Problem w tym, że entropia źródeł wówczas maleje.

Aby umożliwić łatwiejsze zrozumienie w jakich warunkach możliwe jest malenie entropii źródeł, przypomnijmy przebieg rozwoju pojęcia entropii.

Jej historia zaczęła się na początku XIX wieku, kiedy Leonard Sadi Carnot próbował określić relację jaka zachodzi między ilością ciepła dostarczonego maszynie a ilością uzyskanej z niego pracy. Pojęcie ciepła nie było jeszcze wówczas tak sprecyzowane jak dzisiaj i Carnot w swej pracy posłużył się terminem "caloryk", pochodzącym od Lavoisiera. Potraktował różnicę temperatur między kotłem a skraplaczem maszyny parowej jak różnicę poziomów wody u szczytu i podnóża wodospadu. Stąd ilość możliwej do uzyskania pracy widział jako iloczyn tej różnicy temperatur i ilości dostarczonego kaloryka. W tak rozumianych obliczeniach kaloryk nie przedstawiał energii, lecz wielkość, którą w przyszłości Clausius nazwał entropią. Carnotowi oprócz sformułowania problemu sprawności termicznej udało się wykazać, że największą sprawność będzie miała maszyna działająca bez strat a więc jak to określił - odwracalnie.

W połowie XIX wieku problematyką ciepła zajął się Rudolf Clausius, który sprecyzował pojęcie ciepła i sformułował pierwszą zasadę termodynamiki. Potem zebrawszy prace Carnota, Clapeyrona oraz Kelvina , wyprowadził z nich drugą zasadę termodynamiki, której nadał postać całki kołowej z funkcji nazwanej przez siebie entropią. Stało się wówczas jasne, że urządzenie zamieniające ciepło na pracę może mieć tylko ograniczoną sprawność, zależną jedynie od temperatury grzejnika i skraplacza. Z własności entropii wynikało, że jej wartość nie zależy od rodzaju czynnika, i że w układach odosobnionych musi w czasie przemiany wzrastać. Było to konsekwencja przepływu ciepła (ex definitione) ze spadkiem temperatury i tarcia (nieuniknionego). Clausius ogłosił też wnioski filozoficzne wynikające z drugiej zasady: wszystkie przemiany w przyrodzie, w których bierze udział ciepło są nieodwracalne. Temperatury się wyrównują a Wszechświat czeka w dalekiej przyszłości śmierć cieplna.

Ogłoszenie drugiej zasady termodynamiki spowodowało ujawnienie sprzeczności przy zestawieniu jej z mechaniką klasyczną. Równania mechaniki były odwracalne ze względu na czas - po zmianie czasu na ujemny równania opisywały przebieg wydarzeń wstecz, czyli żaden kierunek przebiegu zdarzeń nie był wyróżniony. Zrozumienie, że druga zasada wyróżnia kierunek przepływu czasu a mechanika nie, zapoczątkowało długie spory w świecie fizyków i filozofów, które dopiero prace Ludwiga Boltzmanna pomogły rozstrzygnąć. W 1872 roku ogłosił on swoje słynne twierdzenie H, które orzekało, że entropia nie maleje. W twierdzeniu tym H można utożsamić z entropią termiczną, mimo, że zostało ono wyprowadzone w oparciu o model mechaniczny. Pogodzenie sprzeczności możliwe było na gruncie interpretacji statystycznej: wszystkie rozkłady elementarne są równie prawdopodobne, ale rozkłady o większej entropii mogą być realizowane na więcej sposobów i dlatego są w sumie bardziej częste. Od tej chwili pozycja drugiej zasady była ugruntowana, choć nie rozumiano jej tak kategorycznie jak poprzednio. Do czasu.

W pierwszych latach XX wieku prace Waltera Nernsta wykazały, że entropia wyliczona w oparciu o model gazowy, jak w równaniu H Boltzmanna, jest nie do pogodzenia z zachowaniem faz skondensowanych w pobliżu zera bezwzględnego. Zaowocowało to wprowadzeniem do termodynamiki trzeciej zasady głoszącej, że w zerze bezwzględnym należy przyjmować entropię równą zero. W rezultacie dzisiaj godzi się te zasady stwierdzeniem, że druga zasada pozwala wyliczyć przyrosty entropii i określić kierunek przemiany a trzecia pozwala wyznaczyć jej wartość bezwzględną.

W tym samym czasie C. Caratheodory pokusił się o bardziej klarowne (z punktu widzenia teorii) przedstawienie termodynamiki. Stwierdził, że nie jest potrzebne pojęcie ciepła jako osobnej formy energii. Wystarczy stwierdzenie, że jest to różny od pracy przekaz energii wewnętrznej. Ale ani przekaz energii drogą pracy, ani ten drugi sposób nie jest różniczką zupełną, czyli zawsze zależą one od drogi przemiany. Caratheodory stwierdził, że istnieją przemiany graniczne, jednak nie to jest ważne dla naszych rozważań a tylko fakt, że przemiany te są zawsze kolejnymi stanami równowagi.

Uświadomienie sobie przez fizyków, że opis termodynamiki klasycznej nie nadaje się do analizy układów nie będących w stanie równowagi termodynamicznej wymusił sformułowanie nowego formalizmu nazwanego termodynamiką nierównowagową. Formalizm ten radykalnie różni się od stosowanego w termodynamice klasycznej: przestrzeń stanów jest zastąpiona przestrzenią fizyczną a czynnik fenomenologiczny, materią o budowie cząstkowej. Pojawiają się "źródła entropii", które nie mają analogii w termodynamice klasycznej. Gradient wielkości intensywnych wywołuje przepływy, czyli procesy nieodwracalne. Iloczyn takiego "bodźca" termodynamicznego i skoniugowanego z nim przepływu jest traktowany jako źródło entropii. Przepływy mogą się sumować lub niwelować poprzez procesy sprzężone. Gdy np. dochodzi do przepływu ciepła, to może zdarzyć się, że w układzie wywoła on przeciwnie skierowany przepływ składników powodujący powstanie gradientu stężeń. Termodynamika nierównowagowa najefektywniejszych modeli dostarcza dla stanów układu ustalonych w czasie, i niewiele odchylonych od stanu równowagi. Spełniony jest wówczas w pełni postulat lokalnej równowagi komórkowej konieczny dla stosowania liniowych metod obliczeniowych.

Trzeba zdawać sobie sprawę, że identyczność entropii klasycznej i nierównowagowej jest względna, podobne jak względne jest pojęcie ruchu. Entropia klasyczna przepływa razem z ciepłem lub czynnikiem, natomiast entropia nierównowagowa jest produkowana lokalnie. W teorii klasycznej są układy, których entropia może maleć kosztem innych w których rośnie - w nierównowagowej rośnie wszędzie, ale za to istnieją procesy w których entropia może maleć kosztem wzrostu w innych procesach (zachodzących w tym samym obszarze). W termodynamice klasycznej ostateczny bilans dotyczy tylko źródeł ciepła; w nierównowagowej określany jest wzrost entropii układu. Termodynamicy "klasyczni" przystępując do badań wyodrębniają z otaczającego go świata układ, który badają a resztę nazywają otoczeniem. W teorii klasycznej nie precyzuje się takich parametrów otoczenia (czyli źródła ciepła) jak skład chemiczny, objętość czy ciśnienie a jedynie określa się temperaturę. Mocno podkreśla się przy tym, że wszystkie ustalenia teorii klasycznej dotyczą tylko układów zamkniętych. Termodynamicy "nierównowagowi" wyodrębniając układ badany, większą uwagę zwracają na granice tego układu. Układ taki może się przemieszczać a przez jego ścianki mogą przepływać substraty, produkty i substancje obojętne, ale to co dzieje się poza układem, termodynamików nie interesuje. Jednak mimo tak elastycznego podejścia do badań, termodynamika układów żywych wydawała się sprzeczna.

W roku 1937 na Uniwersytecie w Chicago, wiedeński biolog Ludwig von Bertalanffy po raz pierwszy przedstawił zarys ogólnej teorii systemów. Pokazał, że niektóre systemy otwarte takie jakimi są np. zwierzęta, działają wbrew drugiej zasadzie termodynamiki w sensie wzrostu entropii chemicznej. Chociaż wszystkie przemiany ustroju przebiegają ze spadkiem charakteryzujących je parametrów, to jednak ogólnie biorąc entropia organizmu nie rośnie. Paradoks ten nie rozwiązany był aż do prac Ilyi Prigogine'a, który wykazał, że pewne układy otwarte (nazywane strukturami dysypatywnymi) są w termodynamice czymś wyjątkowym i chcąc uniknąć sprzeczności trzeba je traktować inaczej, niż czyniła to termodynamika ze zwykłymi układami przepływowymi. Struktury dysypatywne, czyli układy otwarte trzeciej klasy charakteryzują się wymianą materii i energii z otoczeniem jak również zachodzeniem w ich obrębie przemian dalekich od stanu równowagi. Przemiany te są we wzajemnej równowadze dynamicznej i cechują się wzajemnym uwarunkowaniem, tak, że Prigogine nazwał je procesami sprzężonymi. Np. w żywym organizmie procesy sprzężone prowadzą z jednej strony do dezorganizacji wysokoenergetycznych składników pożywienia a z drugiej dzięki nim przebiegają procesy umożliwiające funkcje ruchowe i budulcowe organizmu. Struktury dysypatywne są układami w których nie da się stosować metod liniowych, gdyż procesy sprzężone są dla siebie nawzajem "układami odniesienia". Nieprzydatna jest w nich zasada przemienności Onsagera, gdyż struktury te są anizotropowe, mimo stacjonarności zachodzących w nich procesów. Termodynamice struktur dysypatywnych udało się ustalić, że mimo, iż w stanie stacjonarnym produkcja entropii jest minimalna, istnienie struktury uzależnione jest od dopływu energii (ujemnej entropii) z zewnątrz.

Można by w tym miejscu stwierdzić, że metoda Prigogine'a zasadniczo umożliwiła wyjaśnienie paradoksu Bertalanffiego z jednym wyjątkiem, jakim jest chloroplast roślin zielonych.

W 1988 roku trzech niemieckich uczonych dostało nagrodę Nobla za wyjaśnienie szczegółów budowy ośrodka reakcji w którym przebiega fotosynteza. Dzięki temu wiemy, że struktury chlorofilowe w chloroplaście wokół tzw.centrum reakcji wyłapują kilka nisko energetycznych kwantów światła po to, by rozpędzić jeden elektron. Zyskuje on energię potrzebną do wytworzenia takiej różnicy potencjałów między wewnętrzną i zewnętrzną powierzchnią błony chloroplastu, jaka umożliwia rozkład cząsteczki wody. W tym procesie entropia maleje.

Podsumujmy. Termodynamika klasyczna analizuje przyrosty entropii źródeł, termodynamika nierównowagowa oblicza produkcję entropii w układzie, teoria struktur dysypatywnych usiłuje uzgodnić bilans wzrostu entropii w procesach sprzężonych z przyrostem entropii otoczenia. Ale to co powiedzieliśmy o rozwoju pojęcia entropii nie daje jeszcze wyobrażenia o możliwości jej malenia, dlatego zwróćmy uwagę na dwa momenty ważne przy stosowaniu potencjałów.

Potencjał wprowadzony został przez Lagrange'a do opisu pola sił, w którym praca przemieszczenia cząstki nie zależy od drogi. Tak sformułowany potencjał jest funkcją odległości niezależną od czasu. Dzięki twierdzeniu Gaussa pojawiła się wersja strumieniowa potencjału. To par exellence matematyczne twierdzenie, dzięki hydraulicznej interpretacji pozwoliło powiązać zmiany energii potencjalnej z przepływem nieściśliwej cieczy. Istnieje jeszcze inne twierdzenie Gaussa pozwalające całkę strumieniową po powierzchni określić przez całkę objętościową z divergencji, w tym samym obszarze. Jest bardzo ważne, aby zdawać sobie sprawę iż są to trzy wersje tego samego potencjału, funkcji bezźródłowej a więc nadającej się do opisu tylko układów zamkniętych i odosobnionych. Trzeba również zdawać sobie sprawę jaką fizyczną interpretację mają źródła w teorii potencjału: jest to pojawienie się "dodatkowej" energii w układzie.

Wiadomo z mechaniki, że można zawsze problem dwóch ciał sprowadzić do problemu jednego ciała i rozwiązać go. Ale już problem ogólnego ruchu trzech ciał, jest do dzisiaj nie rozwiązany. W dowolnym ruchu trzech ciał powiązanych siłami potencjału grawitacyjnego nie potrafimy stwierdzić, czy w przyszłości jedno z ciał nie opuści układu. Dotyczy to również sytuacji odwrotnej i dlatego do dzisiaj ważne są słowa Maxa Borna, iż nie wiemy skąd cząsteczki gazu wiedzą kiedy mają zacząć kondensację. Chcę przez to powiedzieć, że nie mamy teorii łączącej parametry cząstek na powierzchni potencjału z parametrami cząstek, które go opuściły.

Zauważmy, że potencjały możemy z grubsza podzielić na dwa rodzaje:

- potencjały naturalne, np. związane z siłą elektromagnetyczną lub grawitacyjną, których nie umiemy do siebie dodawać,

- potencjały pomocnicze takie jak entalpia, energia swobodna, itp., które potrafimy przeliczać jedne na drugie.

Przeliczanie potencjałów pomocniczych jest możliwe, bo są miernikami tylko energii kinetycznej molekuł, natomiast potencjały naturalne, manifestują istnienie naturalnych, niezależnych sił. Energia kinetyczna, której wyrazicielem jest temperatura nie może być ujemna, może się zatem tylko dewaluować - za to energia kinetyczna ciał w polu grawitacyjnym może zmieniać się w energię potencjalną, a elektryczna może zmieniać się w magnetyczną. I w jednym i drugim wypadku obojętne jest jak przyjmiemy układ odniesienia - rachunki nie obejmują punktów osobliwych oznaczających dodatnie lub ujemne źródło.

To pozwala jasno określić trudności w uzyskaniu równania stanu dla gazów, opisujące skraplanie. Oddziaływania elektryczne określone przez potencjał, np. van der Waalsa, są "statyczne". Przy prędkości światła z jaką się rozchodzą można powiedzieć, że nie zależą od prędkości atomów. Oddziaływania termiczne są bezwładnościowe - zależą od masy i prędkości cząstki, są zatem potencjałem "kinematycznym" a więc całkiem innej natury. Gdybyśmy potrafili je dodać do siebie, potrafilibyśmy znaleźć zerowanie sumarycznego potencjału, lecz oznaczałoby to, że po pierwsze umiemy rozwiązać problem nieinercyjnych układów odniesienia, po drugie umiemy wykreślić pole sił wokół dowolnie rozłożonych oddziałujących cząstek. A jednak cząsteczki rozwiązują ten problem. A zatem; skoro są powiązane w cieczy, siłami potencjału (statyczno-kinematycznego), równanie stanu w punkcie parowania musi zawierać osobliwość. Oznacza to, że prawidłowe równanie stanu powinno być nie tak jak obecnie równaniem termicznym a tylko termiczno - kalorycznym.

Cząsteczka wydostając się z cieczy do pary doznaje skoku potencjału, co dawniej określano, że pochłania utajone ciepło parowania. Tym samym cząsteczka pary posiada nie tylko energię kinetyczną ale również ukrytą energię, którą może transportować niezależnie od temperatury.

Popatrzmy na rysunek.

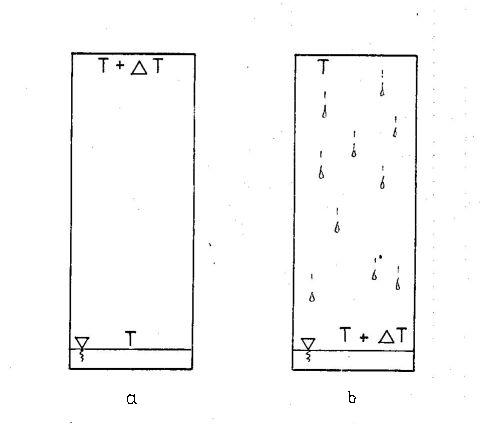
W zamkniętym naczyniu znajduje się ciecz i jej para. (a)

Jeżeli u góry naczynia temperatura będzie wyższa niż na dole, przenikanie ciepła będzie odbywało się bardzo powoli. Jeżeli jednak wyższa temperatura będzie na dole (b) i wystąpi parowanie to transport energii będzie odbywał się błyskawicznie, gdyż wytworzy się obieg - do góry popłynie para a na dół krople cieczy. Przepływ odbywał się będzie dzięki "znikaniu" pary na górnej powierzchni i będzie miał miejsce niezależnie od tego, czy w naczyniu znajduje się inny gaz.

Warunkiem aby obieg miał miejsce jest różnica temperatur u góry i dołu naczynia. Ale trudno jest sprecyzować parametry czynnika w czasie tej "przemiany termodynamicznej". Jeżeli rozwiniemy powierzchnię poruszających się w dół kropli np. przez wypełnienie naczynia siatkami, to zauważymy wymianę masy i ciepła przez ciecz i jej parę. Sądzę, że można przemianę jakiej nawzajem podlegają, nazwać sprzężoną ale w termodynamice nie sposób znaleźć narzędzi przy pomocy których można by ją policzyć. Mimo stacjonarności i prostoty takiego obiegu stajemy w obliczeniach przed trudnością nie do pokonania, jaką jest różne znacznie nadawane przez nas rachunkom. Przy pomocy różnych postaci potencjału możemy policzyć stopień degradacji energii kinetycznej - tutaj najistotniejszą zmienną jest szybkość przemieszczenia czynnika w przestrzeni, w zależności od zmiany różnych uwarunkowań przepływu. Nie muszę przypominać, że termiczna prędkość cząsteczki nie ma rachunkowo nic wspólnego z prędkością strumienia czynnika. Sprawa jeszcze się komplikuje w obecności obcego gazu.

Termodynamika nierównowagowa i chemia fizyczna, dla wyrażenia przyczyny przepływu pary przez gaz, używają określenia różnicy stężeń lub ciśnień cząstkowych. Przy takim sformułowaniu lingwistycznym wręcz nie można sobie wyobrazić ruchu par czynnika w kierunku wyższych stężeń lub ciśnień bez wyraźnej siły napędowej. Tymczasem zjawisko może polegać na zwykłym różnicowaniu prędkości dwóch przeciwbieżnych procesów.

Spójrzmy na rysunek.

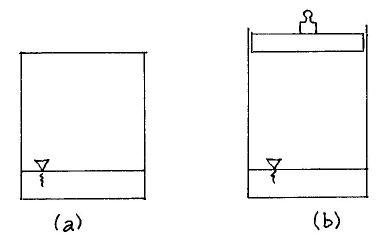
W zamkniętym naczyniu (a) umieszczono wodę przykrytą cieniutka warstwą oliwy a nad nią znajduje się suche powietrze o tej samej temperaturze.

Jeżeli warstwa oliwy ulegnie przerwaniu, woda natychmiast zacznie parować, aż do osiągnięcia przez parę ciśnienia nasycenia. Całkowite ciśnienie wzrośnie, zaś temperatura układu nieco zmaleje. Tę przemianę potrafimy opisać w oparciu o prawo przesunięć równowagi. Ale jeżeli naczynie przykryte będzie tłokiem (b) , to zauważymy, że tłok się uniesie, a tej przemiany nie potrafimy policzyć explicite. Ale nie o rachunki tu idzie. Najważniejsze jest, że nie powietrze ze swoją temperaturą jest "warunkiem" równowagi, tylko możliwość parowania. Będzie ono zachodziło tak długo aż ciśnienie pary w sąsiedztwie powierzchni wody, osiągnie wartość nasycenia odpowiednią danej temperaturze. O sile i niezależności tego procesu przekonałem się w 1968 roku, kiedy to na mój wniosek Energopomiar wykonał w elektrowni Halemba badanie chłodni kominowej z odciętym dopływem powietrza do chłodzenia. Chłodnia działała! Oczywiście było to możliwe dzięki odpływowi w górę pary poprzez dyfuzję, nie mniej oficjalna teoria chłodni nie analizuje takiej możliwości.

Chcę w tym miejscu raz jeszcze zwrócić uwagę na różnice pojęcia równowagi między cieczą i parą. Na rys. 2(b) mamy do czynienia z równowagą dynamiczną procesu stacjonarnego a na rys. 3(a) z równowagą statyczną.

Równowaga dynamiczna charakteryzuje się pewną szybkością, stosunkiem wolumenu pary do czasu. Zatem jeżeli parująca woda porusza się względem powietrza to można porównywać szybkość przepływu tej stygnącej wody z szybkością strumienia wytworzonej z niej pary. Można zatem wyobrazić sobie sytuację w której szybkość przepływu wody względem chłodnego, wilgotnego powietrza będzie mniejsza niż skierowana w drugą stronę szybkość strumienia właśnie wytworzonej pary względem tego powietrza. Zestawienie dwóch wspomnianych procesów da zjawisko wymiennika przeciwprądowego.

W ten sposób dotarliśmy do momentu w którym przemiany zachodzące w cieplnicy przestają być tajemnicze. Przepływ w kolumnie mający charakter wymiany przeciwprądowej jest aktem dynamicznej separacji uczestników procesu: gorącej pary i zimnej wody. Separacja ta umożliwia "puchnięcie" strumienia pary w czasie przepływu, dzięki brakowi sprzężenia zwrotnego, jakim jest wzrost ciśnienia w układzie po akcie odparowania.

Pozbawienie obiegu dwustrumieniowego jego tajemniczości nie rozwiązało podstawowego problemu: jak liczyć entropię? Suma entropii źródeł przy obliczeniu bilansu wykazuje malenie. Nie można traktować cieplnicy jako struktury dyspatywnej, bo entropia w niej nie maleje kosztem otoczenia.

Wymiana przeciwprądowa ciepła i masy jest procesem nieliniowym, a chociaż entalpie pary i wody pozwalają zbilansować kolumnę nie dają podstaw do budowy teorii. Dawniej sądziłem, że taką podstawą może być pompa ciepła Carnota, której sprawność jest zawyżona z powodu wpływu pola grawitacji. Dzisiaj nie jestem tego taki pewien.

Lektura prac o strukturach dyspatywnych profesora Prigogine'a uświadomiła mi jak bardzo teoria entropii ograniczona jest teorią potencjału. Ale czym się kierować gdy go opuszczamy? Czy krzywa potencjału konkretnego czynnika (medium) biorącego udział w procesie cieplnicowym powinna mieć wpływ na sprawność cieplnicy? Jeżeli cieplnica nie jest pompą ciepła (w sensie Carnota) to jak określić dobroć działania cieplnic?

Mnóstwo tego typu pytań do dzisiaj nie ma odpowiedzi, bo nie było porządnych badań cieplnicy. Wielokrotnie walczyłem o prawidłową interpretację wyników wykonanych pomiarów, gdyż komentarze do badań były zawsze typu "pomiary są błędne, bo przecież entropia nie może maleć". Mimo upływu ponad ćwierćwiecza od czasu zbudowania cieplnicy do niczyjej świadomości nie dotarła możliwość pełnej zmiany ciepła w pracę.

A zatem; skoro druga zasada jest za mocna aby ją obalić, proponuję V Zasadę Termodynamiki: Dane ciało wraz z energią wewnętrzną może być przenoszone w sposób mechaniczny w dowolnym kierunku, niezależnie od zmian temperatury.

Katowice 21.05.1989